How to "Do the DEW" - An Engineer's Guide

Design criteria for a megawatt scale Directed Energy Weapon

Revision 2 - 11/1/2023 : Corrected chart above heatmap showing diffraction-limited beam size diameter as a function of laser wavelength

The Philosophical Bit

I have a confession to make.

When I was a kid I did something so horrible that it still haunts me in my moments of weakness. It didn’t start out as something horrible, though - honest! Rather, it was sheer curiosity that compelled me to pick up my mother’s page-sized (8.5” x 11”) magnifying glass and wonder about what might happen if I took it out into the summer sun.

So, that’s what I did. At first, I was absolutely enthralled by my newly found superpower that allowed me to focus and direct the sun’s rays upon any target of my choosing. I burned leaves, sticks, paper towels and any other organic, inanimate items I could round up. It was great fun!

But then, in a moment that, in retrospect, must have felt something like the monkeys discovering tools in 2001: A Space Odyssey , my eyes fell upon a line of ants marching through the yard in single-file carrying on with their daily foraging activities. There I sat with such a powerful weapon in my hands. What was I to do? Of course, I torched them and watched them shrivel up and reduce to a stream of smoke. I don’t recall feeling any compassion for the creatures I was vaporizing. I only remember feeling amazed at what I was able to accomplish with a simple magnifying glass.

Now that I’m much older and wiser (hopefully!), I think about what I did to those poor ants and how oblivious I was to the fact that I was doing something EVIL! I suppose it is poetic justice that I now find myself in the position of those poor ants.

Yes, that’s right. We are all under siege and in the cross-hairs of Directed Energy Weapons (DEWs) perched high above our heads. If you haven’t come to the same conclusion after the explosion in fires, particularly Maui, over the last couple of years, then this might not be an article you care to read. If, on the other hand, you are like me in reaching this conclusion, or if you still have an open mind about it, then I encourage you to read on.

This is going to be a technical article, but I really want to establish the physical limits of what is possible, and more importantly, NOT possible in terms of DEWs. There is so much rampant speculation about this topic online which I don’t think is tremendously helpful. We need to aim for technical accuracy so that we all have the best idea about what our enemies are up to.

After all, we have something the ants don’t have - we have the ability to use our minds to figure out what is going on and to do something about it!

I hope you will forgive me for burning those ants so long ago.

Now, let’s proceed…

The Problem Statement

The essence of what we need to do is design a weapon that will deliver energy, or more precisely, power (energy per unit time) from a source at some point A to a target at some other point B, which may be located very far away.

How can we transmit power through space? Well, there are a number of different ways this can be done. One might imagine using sonic acoustic waves in the air to transmit power. A similar approach might work for transmitting power in water. But, these methods aren’t very efficient, and moreover, they require the source and target to be surrounded by the same medium (e.g. air, water).

Hands-down the best way to transmit power through space is electromagnetic (EM) radiation. EM radiation travels at the speed of light and can, depending on the wavelength, travel through different media while suffering only a small amount of attenuation. EM radiation also tends to interact very well with different target materials, particularly organics. There is no other choice, really. Power delivery across space, for all practical purposes, requires EM radiation.

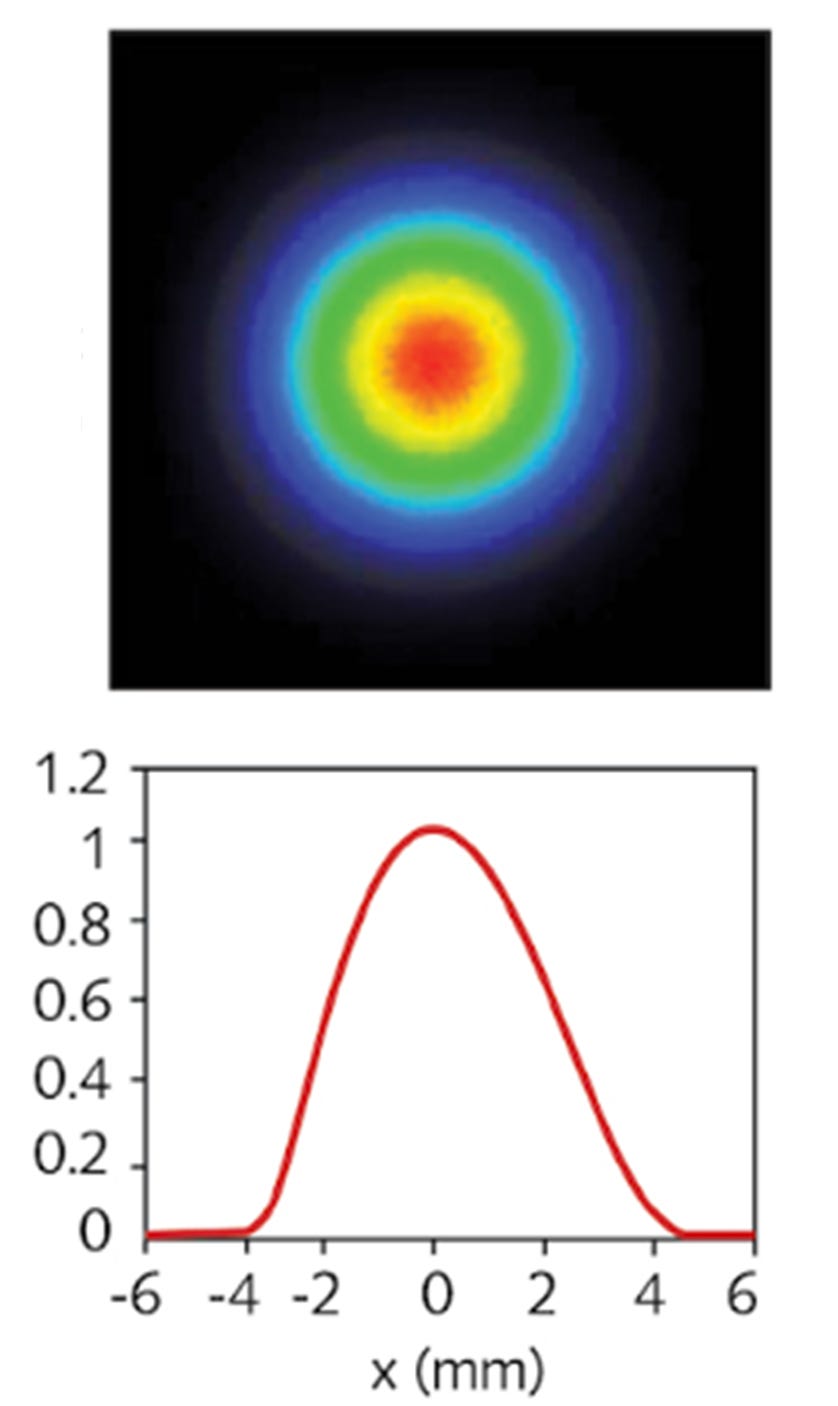
But, we need more than just EM radiation. We need EM radiation that has been concentrated into as tight a beam as possible at the point where it leaves the source. What we really need is a laser, or at the very least, a high-quality Gaussian beam. Almost all laser beams are Gaussian by default. They look something like this in cross-section:

Cross-section of a Gaussian beam

For the purposes of this analysis, it will be assumed that the beam from a DEW is Gaussian and of the highest quality.

Key Considerations for Laser Weapon Design

Now that we’ve established the basic problem we are trying to solve, we can move on to some of the practical considerations that will guide the design. There are five key criteria that we must really think hard about:

Important considerations in the early design phase of a laser weapon for targeting objects on the surface of the Earth.

1. Power density required at target - We first need to define our target and what we would like the laser power to do to it in order to understand how much power needs to be delivered per unit area. My working assumption is that many of the DEWs in existence today have been designed to target organic matter - things like houses, trees, dry brush, etc. The threshold power density for combustion of wood is around 40 W/cm².¹ So, in almost all cases, a DEW that is capable of starting fires is going to need to deliver at least this much power to the target. That is an important idea to let sink in because it is actually a very high value. For comparison, the sun only delivers about 0.1 W/cm² to the Earth’s surface!

2. Wavelength(s) required for target interaction - The wavelength (λ) of light determines the amount of energy (E) carried by each photon by the following equation:

   \(E=hc/\lambda\)

   where h is Planck’s constant and c is the speed of light. The energy calculated by this equation is typically expressed in units of electron-volts (eV). Now, we just need to make sure that whatever it is that we are targeting with our laser has atomic and/or molecular energy level transitions available that match the energy level of the photons in the beam. For low-wavelength light between x-rays and microwaves, this is usually no problem. Nearly all atoms and molecules have oodles of electronic, vibrational and rotational energy levels within this range. Although, the caveat would be that for a very narrow bandwidth beam like a laser, we usually need to make sure that there is at least some absorption by the material at the design wavelength before diving into the design. Now, for very long wavelengths the photon energy decreases to such a low level that there just aren’t any atomic or molecular transitions available. That’s why humans are mostly transparent to radio waves. There are no matching energy levels in the atoms of our bodies to absorb the radiation so they just pass right through. So, it is very important to ensure that our laser weapon operates at a wavelength that can be absorbed by the target. After all, that’s the whole point!

3. Beam diameter at target - There are a couple of reasons why this criteria is important to consider. First, the diameter of the beam at the target determines the power density delivered to it. For a given power output of the laser, the power density will decrease as the beam size increases. Also, operational concerns (e.g. minimizing collateral damage, stealth operation) may place an upper limit on the beam diameter.

   How do we figure out the beam diameter at the target? We can’t just assume that the beam arrives at the target at the same size it was when it left the source, especially when the distances involved are very large. The reason is that whenever we try to squeeze light down into a beam it responds by spreading out. The more we squeeze, the more it spreads out. That’s just how it works. The measure of this spread is called the angular divergence (θ) and it is defined by:

   \(\theta = \lambda/\pi D_{s}\)

   where, λ is the wavelength of the laser and Dₛ is the diameter of the beam as it leaves the source. This equation tells us that we should expect the beam spread to increase as its diameter decreases relative to the wavelength. On the other hand, at very large beam diameters the spread tends toward zero, which implies that the beam size at the target approaches its size at the source. This becomes apparent in the following equation for the beam diameter at the target (Dₜ):

   \(D_{t} = D_{s}\sqrt{1 + \left(\frac{4\theta d}{D_{s}} \right)^2}\)

   where, d is the distance between source and target. We can see how this equation works in the figure below where I’ve plotted the beam diameter at the target and power density as a function of the source diameter assuming a 1 MW green laser at 500 nm wavelength located 250,000 meters away from the target (roughly low-Earth orbit). Interestingly, we can see that there is a minimum in the target diameter and corresponding maximum power density located near a source diameter of 0.38 m (red-dashed line). The target beam diameter at this point is about 0.59 m and the peak power density is almost 800 W/cm². Note that since we have assumed a Gaussian beam, the power is not spread out evenly over the area defined by the target diameter. Instead, it is more concentrated toward the center. Therefore, we can get a rough estimate of the peak power density by simply multiplying power density obtained by assuming the power is spread out evenly by a factor of two.

   

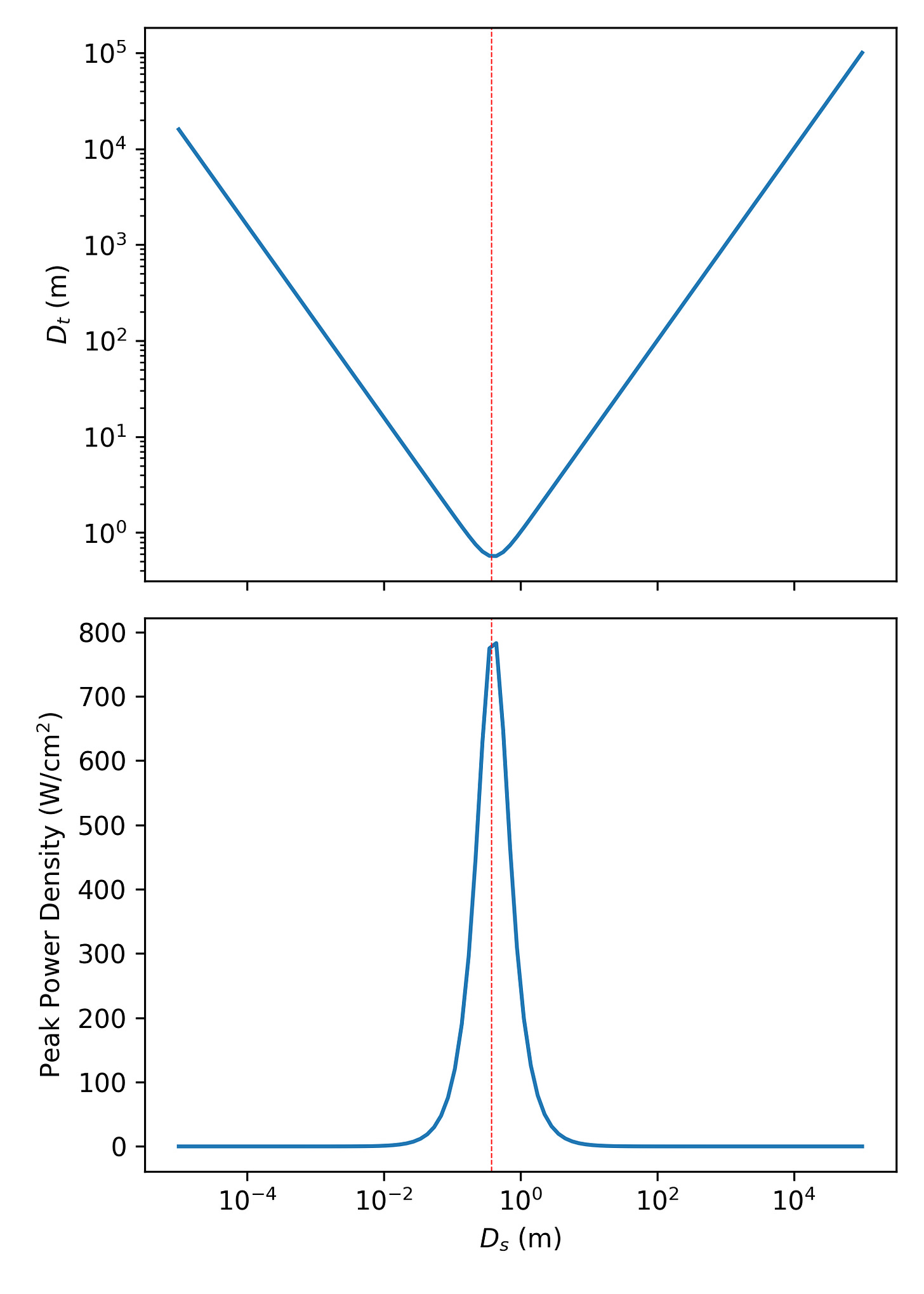
   Target beam diameter and peak power density as a function of source diameter for a 1 MW 500 nm laser located at LEO

   We want to design our laser weapon so that it operates near the maximum power density. That requires us to pay careful attention to the beam size at the target and how it is affected by its wavelength, its size at the source and the distance separating the source and target.

4. Distance between source and target - We saw above how the distance affects the beam diameter and power density at the target. The distance is also important whenever the beam is traveling through an attenuating medium, which is covered next.

5. Attenuation between source and target - We want to maximize the amount of power that makes it from source to target. Therefore, we need to make sure that the intervening path does not significantly attenuate the beam. There are two mechanisms by which a beam can be attenuated: scattering and absorption. The magnitude of attenuation by both mechanisms depends on the wavelength of the laser and the distance the beam travels through the medium. As far as scattering is concerned, shorter wavelengths tend to be scattered more intensely in the atmosphere due to Rayleigh scattering. There may also be scattering by soot and aerosols in the atmosphere. Attenuation by absorption can be avoided by judicious selection of wavelength(s) that have high transmissibility through the atmosphere.

The spectrum of possible DEW designs

All of the considerations discussed in the previous section impose real constraints on the design of DEWs. Most of the commentary I have seen online pertaining to DEWs does not appear to properly account for these constraints. What is the technical basis for commentators stating that DEWs use “nanometer waves” or “5G”? Often, statements like this seem to be pulled directly out of someone’s rear-end. When information is scattered all over the map it becomes nothing but noise that interferes with our ability to properly ascertain the truth.

In my opinion, we need to be as rigorous as possible. To that end, I’ve attempted to map out the realm of possible DEW designs in the figure shown below. This figure is packed with information so please bear with me as I explain everything.

First, there are three separate charts stacked vertically and sharing the x-axis which is the wavelength of the laser used for the DEW. The bottom chart shows the atmospheric transmission spectrum. This is a useful starting point that can help us to quickly see which wavelengths can be transmitted through the atmosphere without suffering significant attenuation. The middle chart is a heat map which displays the peak power density at each combination of wavelength and distance to the target. The peak power density for each point was determined using the method described in the previous section. Horizontal bars of varying widths have been added to denote the most useful scales for weapon design: urban environment, terrestrial aviation, low-Earth orbit and geo-synchronous orbit. Vertical dashed lines have been added to denote the wavelengths of some different laser types. Also, a vertical band has been added to mark the range of wavelengths employed by 5G communications. The diagonal dashed lines are actually contours on the heat map fixed at the power density for wood combustion (40 W/cm²) at various laser output powers. Finally, the top chart shows the diffraction-limited beam diameter at the target for each of the common targeting heights (color-coded to match labels on right-hand side of the heat map). A horizontal bar has been added to this chart to denote the range of what I consider to be practical beam sizes (~50cm to 100m).

Map of possible DEW designs. This is an important chart to spend some time thinking about.

So, what can we learn from this plot? Well, first of all we can quickly ascertain that we should definitely avoid wavelengths less than about 150 nm and between 10 um and 1 mm because all of the power from our DEW would be quickly absorbed by the air.

Ok, what else?

Well, let’s assume that we wish to design a DEW for a terrestrial aviation platform and that we would like to keep the power below 10 kW. Just follow the 10 kW contour down until it intersects with the bottom of the horizontal bar for terrestrial aviation. We see then that wavelengths less than about 20 um will be capable of delivering 40 W/cm² from a terrestrial aviation platform. Cool. We could select any number of lasers for this purpose, including DF, Nd:YAG or He/Ne. And if we check the top chart, we see that at all wavelengths less than 20 um a 10 kW laser will produce a beam diameter at the target that is within (or smaller than) the practical beam size range. There you go. We just designed our first laser weapon!

The case that is of most interest to me is a space-based laser platform. At low-Earth orbit we see that a 10 kW laser just won’t cut it. We need more power! At least 100 kW is needed for a visible or NIR laser. If we bump the power up to 1 MW we can now utilize an infrared laser like CO₂ or DF while still keeping the beam diameter within the practical range. There will be much more discussion on this in the next section.

One more thing before moving on. 5G is an awful beam weapon! First of all, it doesn’t make a lot of sense to me why it is used for communications since it is terribly attenuated by atmospheric absorption. Second, its beam size is so large that it requires on the order of 1 MW just to utilize it in an urban environment to start fires. Note, that number doesn’t even include the power lost due to attenuation. I’m aware that millimeter waves can be used as crowd-control weapons, so I’m not trying to imply that there are no hazards associated with 5G. It’s just that, if starting fires is our goal, 5G just ain’t going to cut it.

The mighty DF laser

DF stands for Deuterium Fluoride. It makes for one hell of a powerful continuous-wave chemical laser. This laser, along with its cousin HF (hydrogen fluoride), formed the backbone of the Star Wars program back in the 80s. The primary defense contractor tasked with the development of the HF/DF laser system was TRW, Inc., formerly based in Ohio. As early as 1985 they had already surpassed the 1 MW scale²:

Newspaper clipping from The Province, British Columbia, Sun March 10, 1985.

The physical principle of the laser, which was discovered back in the late 60s, relies on the reaction of hydrogen or deuterium with fluorine to release tremendous amounts of energy, much of which ends up in a vibrational mode that leads to lasing at infrared wavelengths. Specifically, HF lases at a primary wavelength of 2.5-3.2 um, while DF lases at 3.5-4.2 um. Although the HF laser wavelength is significantly attenuated by atmospheric absorption, the DF laser wavelength lies within a narrow window of very high transmissibility in the infrared region. This makes DF an excellent choice for a space-based laser platform targeting objects on the ground.

I feel strongly that if there are Earth-targeting DEWs circling overhead, they are almost certainly based on the DF laser system. But, don’t just take my word for it. David Carroll, in his 2011 review “Overview of High Energy Lasers: Past, Present and Future?” had this to say³:

HF/DF laser work has stopped in the United States and Russia, but continues in China. These systems have significant energy output-to-weight advantages because of their highly energetic chemical species, and by the same token those chemicals (reactants and products) are logistically problematic for armed forces. However, if space-based platforms are ever again seriously investigated, we will likely see an HF or HF overtone system considered because of the tremendous power-to-weight advantage.

Designing a space-based DF laser

Fortunately, there is sufficient information available in the open literature to gain a fairly realistic idea of what a 1 MW continuous-wave DF laser satellite might look like. I drew heavily from the text by Behrens and Lohn for this exercise⁴. I would definitely point the reader toward this comprehensive overview if he/she is interested in learning more about the details of HF/DF lasers.

So, here’s what I came up with:

Realistic conceptual design of a 1 MW DF space-based laser system. Note that the beam would be invisible since it is in the infrared. It has only been added here as a visual aid.

This particular design is estimated to clock in around 10,000 kg when loaded with fuel, which is well within the capability of the Titan III/IV rockets that flew as early as 1990.

Here’s a cut-away view:

Interior view of space-based DF laser

As you can see, the majority of the interior volume of the satellite is devoted to storage of the reactants required to drive the laser. Apart from that, the largest component is the laser assembly itself.

Another cut-away view:

Cut-away view of the DF laser assembly

The laser assembly really isn’t very complicated. There are three distinguishable compartments: combustion chamber, lasing chamber and exhaust chamber. In the combustion chamber the acetylene fuel (C₂H₂) and nitrogen trifluoride (NF₃) are injected through a bank of nozzles at the back wall of the chamber. The reaction between fuel and oxidizer proceeds rather violently, releasing a great deal of heat. Flame temperatures in the reaction zone can exceed 1500K. The heat from the reaction drives the decomposition reaction of excess NF₃ to release free fluorine (F) atoms. The combustion chamber is pressurized to about 100 psia. The gas is ejected at supersonic velocity into the lasing chamber through an array of tiny orifices situated between the deuterium nozzles that form the dividing wall between the two chambers. The deuterium nozzles spray a mixture of D₂ and helium into the lasing cavity which reacts with the F atoms from the combustion chamber to form vibrationally excited DF. The DF quickly relaxes to a lower vibrational energy level, releasing infrared radiation at 3.5 to 4.2 um. The infrared photons bounce back-and-forth between two gold mirrors situated perpendicular to the gas flow direction. The laser beam exits through a small aperture and travels into the optical system. The optical system consists of a 3-axis turret which allows precise targeting of the beam and a parabolic beam expander which increases the size of the beam to its optimum value of around 1.25 meters (Remember the heat map chart above? That’s where this number came from). When the beam leaves the satellite at a diameter of 1.25 meters it will arrive at the surface of the Earth at a diameter of about 1.9 meters and the peak power density will be around 90 W/cm², which is more than enough to set all kinds of organic matter on fire as many organics strongly absorb IR in the range of 3.5 to 4.2 um.

As mentioned above, this laser is designed to operate as a continuous-wave laser, meaning that the output power remains steady at 1 MW as long as fuel is being provided to the laser assembly. In actual operation, though, you wouldn’t want to run this for long periods of time, say, more than 10 seconds. Most of the heat generated by the reactions is moved out through the exhaust, but there would still be some left over which could overheat some components if the laser is left running for too long. An ammonia-based cooling loop has been provided to remove heat from the most sensitive areas which would greatly improve the safety margin of the system.

If we assume an average shot-time of 3 seconds, then there is sufficient fuel on-board for about 100 shots before refueling is required. If you think about it, if each shot represents a fire set over a 1.9 meter diameter area then you can certainly cause a lot of damage with a single load of fuel!

Disclaimer: I want to make it clear that, although I am an engineer, design of space-based weaponry is not my specialty. However, I have spent a great deal of time thinking through a lot of the technical details and feel that I’m probably not too far off the mark with the conceptual design I have presented. As always, I welcome criticism and feedback, particularly as it may relate to my assumptions and calculations.

A note regarding pulsed lasers

I wanted to briefly comment on some of the commentary I have seen people making regarding “trillion-watt lasers” being used as DEWs. First, it should be clear that it is currently not possible to make a continuous-wave laser with an output power anywhere near 1 trillion watts. It is, however, possible to make femtosecond pulsed lasers that can achieve peak power levels this high and the military has apparently been developing such weapons. As far as using pulsed lasers to start fires, it isn’t clear to me that this would work very well. Pulsed lasers are commonly used to ablate material since the very rapid pulses deposit energy in an extremely small surface layer of the target. They are not very good at depositing energy in the bulk of the target, which would be necessary to initiate combustion. At this point, I am skeptical that pulsed-laser DEWs would be useful as fire-starters.

Conclusion

I hope that I have presented a coherent and persuasive argument here that not only are DEWs technically possible, they aren’t even that difficult to design, build and launch into low-Earth orbit. I am eternally hopeful that we can stop the maniacs who are aiming and firing these weapons upon all of us helpless ants.

1. Waterworth, Michael D.. “Laser Ignition Device and Its Application to Forestry, Fire and Land Management.” (1987).

2. The Province. Vancouver, British Columbia. Sun March 10, 1985. Page 21.

3. Carroll, D.. “Overview of High Energy Lasers: Past, Present, and Future?” (2011).

4. Behrens, Wilhelm H. and Peter D. Lohn. “Hydrogen and Deuterium Fluoride Chemical Lasers.” Gas Lasers (2018): 341-360.